Temporal network classes¶
Undirected and unweighted temporal networks are composed of \(N\) nodes and up to \(m_{\mathrm{max}}=N(N-1)/2\) edges, where each edge \((i,j)\) can be described as a series of events where the edge is either switched on or switched off. One way of expressing that is to define the temporal adjacency matrix
In tacoma, we will interpret temporal networks as if they were recorded in an experiment. We expect that over the course of time \(t_0\leq t < t_\mathrm{max}\) in which we recorded activity, we encountered \(N\) nodes from the node set \(V=\{0,1,\dots,N-1\}\) (nodes possess an integer label). However, nodes do not need to be active (i.e. connected to other nodes) during the time of the experiment to be considered in the node set.
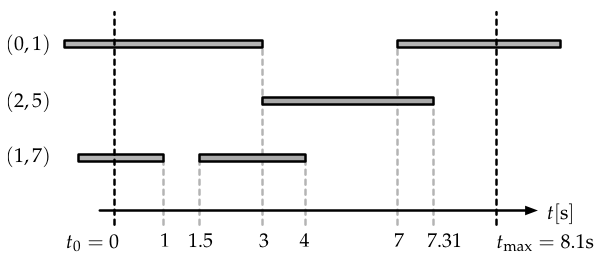
A temporal network and how it was recorded in an experiment. We additionally assume to know that the network consists of \(N=8\) nodes. Edges existed before we started measuring. An edge is considered to be “on” when it exists, shown as a grey bar in this figure. Each time an edge is switched “on” or switched “off”, respectively, the network structure changes and hence this event is recorded. Here, the experiment ends before the edge \((0,1)\) is switched off.
The experiment begins at time \(t_0\), where the network consists of an edge set \(E_0 \subseteq \{i,j: V\times V, i<j\}\). Then, each time the network changes, we denote that time by an entry in a time vector \(t\). Each entry in the time vector corresponds to a network change event and thus to a change in the edge set. We call the total number of change events \(N_e\), such that the vector \(t\) has \(N_e\) entries. In between consecutive times, the network is constant. After the last recorded event, we kept the experiment running until the maximum time \(t_\mathrm{max}\) without observing any change and stopped recording at \(t_\mathrm{max}\).
There’s three data structures implemented in this package, all of which capture the situation described above in different ways and are useful in different situations.
Edge lists¶
The class _tacoma.edge_lists consists of a collection of complete edge lists,
each time the network changes, a complete edge list of the network after the change is saved.
It has the following attributes.
- \(N\) : The total number of nodes
- \(t\) : A vector of length \(N_e+1\). The 0-th entry contains the time of the beginning of the experiment \(t_0\)
- edges : A vector of length \(N_e+1\) where each entry contains an edge list, describing the network after the change which occured at the corresponding time in \(t\). The 0-th entry contains the edge list of the beginning of the experiment at \(t_0\)
- \(t_\mathrm{max}\) : The time at which the experiment ended.
- time_unit : A string containing the unit of time used for the recording.
- notes : Additional notes concerning the experiment.
- int_to_node : A dictionary mapping the node integers to string descriptors. This map can be empty. The map is supposed to be one-to-one.
The network described in the figure above would be recorded as
import tacoma as tc
tn = tc.edge_lists()
tn.N = 8
tn.t = [ 0.0, 1.0, 1.5, 3.0, 4.0, 7.0, 7.31 ]
tn.tmax = 8.1
tn.edges = [
[ (0, 1), (1, 7) ],
[ (0, 1) ],
[ (0, 1), (1, 7) ],
[ (2, 5), (1, 7) ],
[ (2, 5) ],
[ (0, 1), (2, 5) ],
[ (0, 1) ]
]
tn.time_unit = 's'
tn.notes = 'This experiment was conducted as a test.'
tn.int_to_node = {
0 : 'Alice',
1 : 'Bob',
2 : 'Clara',
3 : 'Darren',
4 : 'Elle',
5 : 'Felicitas',
6 : 'George',
7 : 'Harriett',
}
Edge changes¶
The class _tacoma.edge_changes consists of a collection of both edges being created
and edges being deleted.
It has the following attributes.
- \(N\) : The total number of nodes.
- \(t_0\) : The time of the beginning of the experiment.
- \(t\) : A vector of length \(N_e\), each time corresponding to a change in the network.
- \(t_\mathrm{max}\) : The time at which the experiment ended.
- edges_initial : The edge list of the beginning of the experiment at \(t_0\).
- edges_in : A list containing \(N_e\) entries. Each entry is a list of integer tuples, describing the edges being created during this event.
- edges_out : A list containing \(N_e\) entries. Each entry is a list of integer tuples, describing the edges being switched off during this event.
- time_unit : A string containing the unit of time used for the recording.
- notes : Additional notes concerning the experiment.
- int_to_node : A dictionary mapping the node integers to string descriptors. This map can be empty. The map is supposed to be one-to-one.
The network described in the figure above would be recorded as
import tacoma as tc
tn = tc.edge_changes()
tn.N = 8
tn.t0 = 0.0
tn.t = [ 1.0, 1.5, 3.0, 4.0, 7.0, 7.31 ]
tn.tmax = 8.1
tn.edges_initial = [ (0, 1), (1, 7) ]
tn.edges_in = [
[],
[ (1, 7) ],
[ (2, 5) ],
[],
[ (0, 1) ],
[]
]
tn.edges_out = [
[ (1, 7) ],
[],
[ (0, 1) ],
[ (1, 7) ],
[],
[ (2, 5) ]
]
tn.time_unit = 's'
tn.notes = 'This experiment was conducted as a test.'
tn.int_to_node = {
0 : 'Alice',
1 : 'Bob',
2 : 'Clara',
3 : 'Darren',
4 : 'Elle',
5 : 'Felicitas',
6 : 'George',
7 : 'Harriett',
}
Edge trajectories¶
The class _tacoma.edge_trajectories consists of a collection of
_tacoma.edge_trajectory_enry, one for each edge in the network
which was active at least once during the experiment.
Each of those entries has attribute .edge containing the edge it is attributed to.
The second attribute of each
entry, .time_pairs is a list of pairs of doubles, each pair representing
a time interval in which the edge was active.
It has the following attributes.
- \(N\) : The total number of nodes.
- \(t_0\) : The time of the beginning of the experiment.
- \(t_\mathrm{max}\) : The time at which the experiment ended.
- trajectories : A list of
_tacoma.edge_trajectory_enry, as described above. - time_unit : A string containing the unit of time used for the recording.
- notes : Additional notes concerning the experiment.
- int_to_node : A dictionary mapping the node integers to string descriptors. This map can be empty. The map is supposed to be one-to-one.
- edge_similarities (Optional) : A dictionary of Tuple[Int, Int] -> double containing
the similarities of two edges. The integers in the pairs correspond to the index of the edges
in trajectories. This dictionary is computed when
_tacoma.edge_trajectoriesis generated from a conversion usingtacoma.api.get_edge_trajectories()withreturn_edge_similarity = True.
The network described in the figure above would be recorded as
import tacoma as tc
traj = tc.edge_trajectories()
entry = tc.edge_trajectory_entry
traj.N = 8
traj.t0 = 0.0
traj.tmax = 8.1
traj.trajectories = [
entry( (0,1), [(0., 3.), (7.0, 8.1)] ),
entry( (2,5), [(3., 7.31)] ),
entry( (1,7), [(0., 1.), (1.5, 4.0)] ),
]
traj.time_unit = 's'
traj.notes = 'This experiment was conducted as a test.'
traj.int_to_node = {
0 : 'Alice',
1 : 'Bob',
2 : 'Clara',
3 : 'Darren',
4 : 'Elle',
5 : 'Felicitas',
6 : 'George',
7 : 'Harriett',
}
List of adjacency matrices¶
For some cases it might be useful to actually have matrices in memory (e.g. to
compute the epidemic threshold in SIS-models). tacoma offers the possibility to
convert instances of _tacoma.edge_lists and _tacoma.edge_changes
to tacoma.network_formats.sparse_adjacency_matrices or
tacoma.network_formats.adjacency_matrices.
These classes have the same attributes as _tacoma.edge_lists, but
instead of the attribute edges they have the attribute adjacency_matrices.
Convert a temporal network tn as follows
A = tc.adjacency_matrices(tn)
A = tc.sparse_adjacency_matrices(tn)
Note that you can pass any desired scipy.sparse-matrix class and dtype
to tacoma.network_formats.sparse_adjacency_matrices for matrix construction.
Which class to use¶
Each of the classes above has its specific use cases. Since most algorithms rely on
the actual order of network-changing events, the main classes in tacoma are
_tacoma.edge_lists and _tacoma.edge_changes, meaning that
almost all of the algorithms in this package are specifically implemented for both,
but not for _tacoma.edge_trajectories.
_tacoma.edge_lists is to prefer if you just want to sample an edge list at
a specific time. For _tacoma.edge_changes, you would have to start at the
beginning of the network, then fast forward to that time to obtain an edge list. Edge
lists are often easier to deal with, however, if the inter-event times are rather small
and the network is not sparse, two consecutive edge lists might be overlapping strongly.
Hence, edge changes are often faster to deal with and need less memory. Furthermore,
Algorithms which explicitly rely on edge changes, as e.g. dynamic Gillespie algorithms
are natively faster on _tacoma.edge_changes.
_tacoma.edge_trajectories is preffered for drawing an
tacoma.drawing.edge_activity_plot() or to estimate edge-activity rates.