Verification and conversion¶
Especially when dealing with real-world data we need to verify that our networks are in the right format for further analysis. We also need to convert the formats to each other.
Verification¶
Both _tacoma.edge_lists and _tacoma.edge_changes need to follow
certain restrictions such that all algorithms in the package will work without
error. The restrictions are as follows
- All event times including \(t_0\) and \(t_\mathrm{max}\) need to be in order and none of them must be equal.
- The lists \(t\) and edge_lists must be of equal length (\(t\), edges_in, and edges_out, respectively.
- Each list containing edges must not contain duplicate edges, each edge \((i,j)\) must fulfill \(i<j\), there must not be any self-loops.
- Each edge \((i,j)\) must fulfill \(0\leq i<N\) and \(0\leq j <N\).
- Entries of edges_in and edges_out corresponding to the same event must not contain the same edges (one edge cannot get activated and deactivated at the same time).
- The map int_to_node must either contain no entries, or N entries and has to be one-to-one.
In order to verify that a temporal_network fulfills these conditions, do
>>> tc.verify(temporal_network)
0
The function will return the number of found errors. It will also be very verbose about any errors. Within verification, any edge where \(i>j\) will be swapped such that afterwards, \(i<j\).
Conversion¶
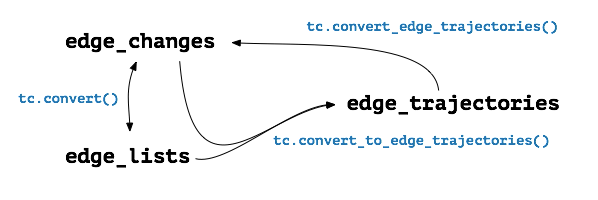
How to convert formats.
For different analyses or algorithms we need temporal networks in different formats. Since edge_lists and edge_changes are the main formats one can convert them to each other easily using
E_L = tc.convert(E_C)
E_C = tc.convert(E_L)
edge_trajectories can be obtained using
E_T = tc.convert_to_edge_trajectories(E_C)
E_T = tc.convert_to_edge_trajectories(E_L)
edge_trajectories can only be converted to edge_changes. This is done by
E_C = tc.convert_edge_trajectories(E_T)