Fundamental properties of cooperative contagion processes
Abstract
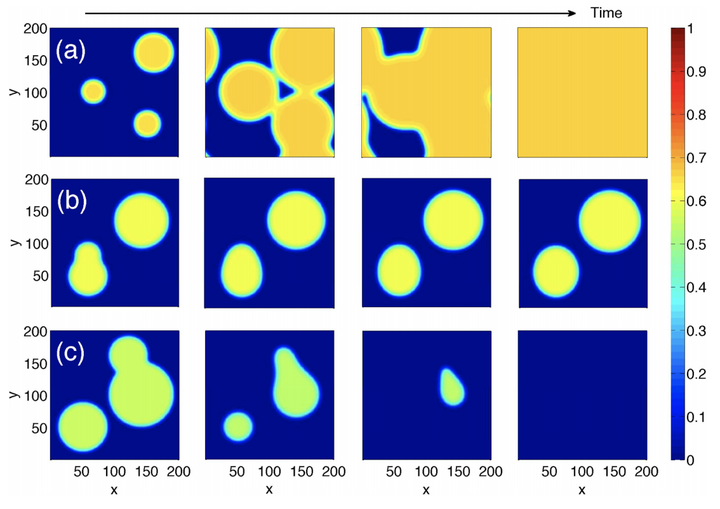
We investigate the effects of cooperativity between contagion processes that spread and persist in a host population. We propose and analyze a dynamical model in which individuals that are affected by one transmissible agent A exhibit a higher than baseline propensity of being affected by a second agent B and vice versa. The model is a natural extension of the traditional susceptible-infected-susceptible model used for modeling single contagion processes. We show that cooperativity changes the dynamics of the system considerably when cooperativity is strong. The system exhibits discontinuous phase transitions not observed in single agent contagion, multi-stability, a separation of the traditional epidemic threshold into different thresholds for inception and extinction as well as hysteresis. These properties are robust and are corroborated by stochastic simulations on lattices and generic network topologies. Finally, we investigate wave propagation and transients in a spatially extended version of the model and show that especially for intermediate values of baseline reproduction ratios the system is characterized by various types of wave-front speeds. The system can exhibit spatially heterogeneous stationary states for some parameters and negative front speeds(receding wave fronts). The two agent model can be employed as a starting point for more complex contagion processes, involving several interacting agents, a model framework particularly suitable for modeling the spread and dynamics of microbiological ecosystems in host populations.